Imagine a seguinte situação:
Área é a denominação dada à medida de uma superfície. Na situação acima estamos nos referindo às áreas da sala e do ladrilho.
Partindo-se deste princípio, o nosso problema se resume ao cálculo da
razão entre as áreas da sala e do ladrilho.
Para que você saiba solucionar, dentre outros, o problema acima, vamos então nos atentar ao método de cálculo da área das figuras geométricas planas mais comuns.
Cálculo da Área do Triângulo
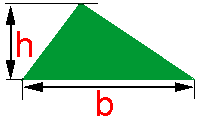
Denominamos de triângulo a um polígono de três lados.
Observe a figura ao lado. A letra h representa a medida da altura do triângulo, assim como letra b representa a medida da sua base.
A área do triângulo será metade do produto do valor da medida da base, pelo valor da medida da altura, tal como na fórmula abaixo:
A letra S representa a área ou superfície do triângulo.
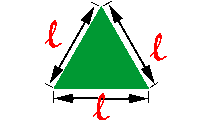
No caso do triângulo equilátero, que possui os três ângulos internos iguais, assim como os seus três lados, podemos utilizar a seguinte fórmula:
Onde l representa a medida dos lados do triângulo.
Exemplos
A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
Do enunciado temos:
Utilizando a fórmula:
A área deste triângulo é 12,25 cm2.
Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
Segundo o enunciado temos:
Substituindo na fórmula:
A área deste triângulo equilátero é de aproximadamente 10,8 mm2.
Cálculo da Área do Paralelogramo
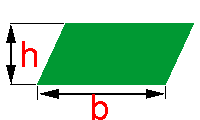
Um quadrilátero cujos lados opostos são iguais e paralelos é denominadoparalelogramo.
Com h representando a medida da sua altura e com b representando a medida da sua base, a área do paralelogramo pode ser obtida multiplicando-se b por h, tal como na fórmula abaixo:
Exemplos
A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
Segundo o enunciado temos:
Substituindo na fórmula:
A área deste polígono é 7,8 dm2.
Qual é a medida da área de um paralelogramo cujas medidas da altura e da base são respectivamente 10 cm e 2 dm?
Sabemos que 2 dm equivalem a 20 cm, temos:
Substituindo na fórmula:
A medida da área deste paralelogramo é 200 cm2 ou 2 dm2.
Cálculo da Área do Losango
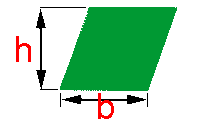
O losango é um tipo particular de paralelogramo. Neste caso além dos lados opostos serem paralelos, todos os quatro lados são iguais.
Se você dispuser do valor das medidas h e b, você poderá utilizar a fórmula do paralelogramo para obter a área do losango.
Outra característica do losango é que as suas diagonais são perpendiculares.
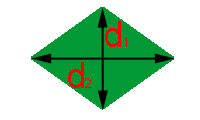
Observe na figura à direita, que a partir das diagonais podemos dividir o losango em quatro triângulos iguais.
Consideremos a base b como a metade da diagonal d1 e a altura h como a metade da diagonal d2, para calcularmos a área de um destes quatro triângulos. Bastará então que a multipliquemos por 4, para obtermos a área do losango. Vejamos:
Realizando as devidas simplificações chegaremos à fórmula:
Exemplos
As diagonais de um losango medem 10 cm e 15 cm. Qual é a medida da sua superfície?
Para o cálculo da superfície utilizaremos a fórmula que envolve as diagonais, cujos valores temos abaixo:
Utilizando na fórmula temos:
A medida da superfície deste losango é de 75 cm2
Qual é a medida da área de um losango cuja base mede 12 cm e cuja altura seja de 9 cm?
Neste caso, para o cálculo da área utilizaremos a fórmula do paralelogramo, onde utilizamos a base e a altura da figura geométrica, cujos valores temos abaixo:
Segundo a fórmula temos:
A medida da área do losango é de 108 cm2.
Cálculo da Área do Quadrado
Todo quadrado é também um losango, mas nem todo losango vem a ser um quadrado, do mesmo modo que todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.
O quadrado é um losango, que além de possuir quatro lados iguais, com diagonais perpendiculares, ainda possui todos os seus ângulos internos iguais a 90°. Observe ainda que além de perpendiculares, as diagonais também são iguais.
Por ser o quadrado um losango e por ser o losango um paralelogramo, podemos utilizar para o cálculo da área do quadrado, as mesmas fórmulas utilizadas para o cálculo da área tanto do losango, quanto do paralelogramo.
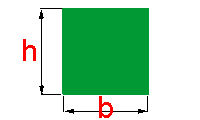
Quando dispomos da medida do lado do quadrado, podemos utilizar a fórmula do paralelogramo:
Como h e b possuem a mesma medida, podemos substituí-las por l, ficando a fórmula então como sendo:
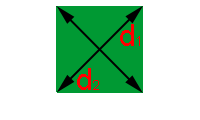
Quando dispomos da medida das diagonais do quadrado, podemos utilizar a fórmula do losango:
Como ambas as diagonais são idênticas, podemos substituí-las por d, simplificando a fórmula para:
Exemplos
A lateral da tampa quadrada de uma caixa mede 17 cm. Qual a superfície desta tampa?
Do enunciado temos que a variável l é igual a 17:
Substituindo na fórmula temos:
Portanto a superfície da tampa desta caixa é de 289 cm2.
A medida do lado de um quadrado é de 20 cm. Qual é a sua área?
Como o lado mede 20 cm, temos:
Substituindo na fórmula temos:
A área do quadrado é de 400 cm2.
A área de um quadrado é igual a 196 cm2. Qual a medida do lado deste quadrado?
Temos que S é igual a 196.
Utilizando a fórmula temos:
Como a medida do lado não pode ser negativa, temos que o lado do quadrado mede 14 cm.
Cálculo da Área do Retângulo
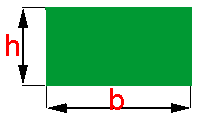
Por definição o retângulo é um quadrilátero equiângulo (todo os seus ângulos internos são iguais), cujos lados opostos são iguais.
Se todos os seus quatro lados forem iguais, teremos um tipo especial de retângulo, chamado de quadrado.
Por ser o retângulo um paralelogramo, o cálculo da sua área é realizado da mesma forma.
Se denominarmos as medidas dos lados de um retângulo como na figura ao lado, teremos a seguinte fórmula:
Exemplos
Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?
Atribuindo 5 à variável h e 25 à variável b temos:
Utilizando a fórmula:
A área deste terreno é de 125 m2.
A tampa de uma caixa de sapatos tem as dimensões 30 cm por 15 cm. Qual a área desta tampa?
Podemos atribuir 15 à variável h e 30 à variável b:
Ao substituirmos as variáveis na fórmula teremos:
Portanto a área da tampa da caixa de sapatos é de 450 cm2.
Cálculo da Área do Círculo
A divisão do perímetro de uma circunferência, pelo seu diâmetro resultará sempre no mesmo valor, qualquer que seja circunferência. Este valor irracional constante é representado pela letra grega minúscula pi, grafada como:
Por ser um número irracional, o número pi possui infinitas casas decimais. Para cálculos corriqueiros, podemos utilizar o valor 3,14159265. Para cálculos com menos precisão, podemos utilizar 3,1416, ou até mesmo 3,14.
O perímetro de uma circunferência é obtido através da fórmula:
O cálculo da área do círculo é realizado segundo a fórmula abaixo:
Onde r representa o raio do círculo.
Exemplos
A lente de uma lupa tem 10 cm de diâmetro. Qual é a área da lente desta lupa?
Como informado no enunciado, o diâmetro da circunferência da lupa é igual a 10 cm, o que nos leva a concluir que o seu raio é igual a 5 cm, que corresponde à metade deste valor:
Substituindo-o na fórmula:
A área da lente da lupa é de 78,54 cm2.
Um círculo tem raio de 8,52 mm. Quantos milímetros quadrados ele possui de superfície?
Do enunciado, temos que o valor do raio r é:
Ao substituirmos valor de r na fórmula teremos:
A superfície do círculo é de 228,05 mm2.
Cálculo da Área de Setores Circulares
O cálculo da área de um setor circular pode ser realizado calculando-se a área total do círculo e depois se montando uma regra de três, onde a área total do círculo estará para 360°, assim como a área do setor estará para o número de graus do setor.
Sendo S a área total do círculo, Sα a área do setor circular e α o seu número de graus, temos:
Em radianos temos:
A partir destas sentenças podemos chegar a esta fórmula em graus:
E a esta outra em radianos:
Onde r representa o raio do círculo referente ao setor e α é o ângulo também referente ao setor.
Exemplos
Qual é a área de um setor circular com ângulo de 30° e raio de 12 cm?
Aplicando a fórmula em graus temos:
A área do setor circular é de 37,6992 cm2.
Qual é a superfície de um setor circular com ângulo de 0,5 rad e raio de 8 mm?
Aplicando a fórmula em radianos temos:
A superfície do setor circular é de 16 mm2.
Cálculo da Área de Coroas Circulares
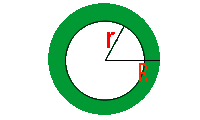
O cálculo da área de uma coroa circular pode ser realizado calculando-se a área total do círculo e subtraindo-se desta, a área do círculo inscrito. Podemos também utilizar a seguinte fórmula:
Onde R representa o raio do círculo e r representa o raio do círculo inscrito.
Exemplos
Qual é a área de uma coroa circular com raio de 20 cm e largura de 5 cm?
Se a largura é de 5 cm, significa que r = 20 - 5 = 15, substituindo na fórmula temos:
A área da coroa circular é de 549,78 cm2.
Qual é a superfície de uma coroa circular com r = 17 e R = 34?
Aplicando a fórmula em temos:
A superfície desta coroa circular é 2723,7672.
Resolução Detalhada do Problema no Começo da Página
Para resolvermos tal problema, primeiramente vamos calcular a área da sala.
Para podermos utilizar a fórmula do cálculo da área de um retângulo, vamos atribuir os 4 m da largura à letra h e os 5,5 m do comprimento à letra b:
Resolvendo através da fórmula:
Agora que sabemos que a sala tem uma área de 22 m2, precisamos conhecer a área do ladrilho.
Como o ladrilho é quadrado, precisamos calcular a área de um quadrado, só que devemos trabalhar em metros e não em centímetros, pois a área da sala foi calculada utilizando-se medidas em metros e não medidas emcentímetros. Poderíamos ter convertido as medidas da sala em centímetros, para trabalharmos apenas comcentímetros. O importante é que utilizemos sempre a mesma unidade (múltiplo/submúltiplo).
A transformação de 25 cm em metros é realizada dividindo-se tal medida por 100:
Então a medida dos lados dos ladrilhos é de 0,25 m.
Se tiver dúvidas sobre como realizar tal conversão, por favor acesse a página que trata sobre as
unidades de medidas, lá você encontrará várias informações sobre este assunto, incluindo vários exemplos e um
link para uma
calculadora sobre o tema.
Voltando ao problema, como o ladrilho é quadrado, a área do ladrilho com lado l = 0,25 é igual a:
Como dito no começo da página, a resolução do problema se resume ao cálculo da
razão entre a área da sala e a área do ladrilho.
Como a sala tem uma área de 22 m2 e o ladrilho de 0,0625 m2, temos a seguinte razão:
Ou seja, para ladrilhar o piso da sala inteira serão necessários ladrilhos 352.
= 
.jpg)
.jpg)
, a um outro número complexo que possui a mesma parte real de z e a parte imaginária o simétrico aditivo da parte imaginária de z .
= 
= 