quarta-feira, 4 de dezembro de 2013
QUESTÃO AOCP
Dos 100 pacientes de um hospital, 52 consomem o medicamento A, 45 consomem o medicamento B e 41 consomem o medicamento C. Além disso, 16 consomem A e B, 17 B e C e 20 consomem A e C. Há pacientes que consomem os três medicamentos, mas 7 não consomem nenhum desses remédios. O número total de pacientes que consomem apenas um dos medicamentos é igual a:
SOLUÇÃO:
Sabemos que:
n(AUBUC) = n(A) + n(B) + n(C) - n(A e B) - n(A e C) - n(B e C) + n(A,B e C) + n(nenhum deles)
100 = 52 + 45 + 41 - 16 - 17 - 20 + x + 7
x = 100 - 92 = 8
Logo consomem apenas A: 52 - 16 - 20 + 8 = 24
Apenas B = 45 - 16 - 17 + 8 = 20
Apenas C = 41 - 17 - 20 + 8 = 12
Consomem apenas 1 medicamento: 24 + 20 + 12 = 56 pessoas
segunda-feira, 4 de novembro de 2013
QUESTÃO DE PORCENTAGEM
Um comerciante comprou certo artigo com um desconto
de 20% sobre o preço de tabela. Em sua loja, ele fixou um
preço para tal artigo, de modo a poder vendê-lo dando aos
clientes um desconto de 25% e a obter um lucro de 40%
sobre o preço fixado. Nessas condições, sabendo que
pela compra de uma unidade desse artigo um cliente terá
que desembolsar R$ 42,00, o seu preço de tabela é
(A) R$ 20,00
(B) R$ 24,50
(C) R$ 30,00
(D) R$ 32,50
(E) R$ 35,00
SOLUÇÃO
de 20% sobre o preço de tabela. Em sua loja, ele fixou um
preço para tal artigo, de modo a poder vendê-lo dando aos
clientes um desconto de 25% e a obter um lucro de 40%
sobre o preço fixado. Nessas condições, sabendo que
pela compra de uma unidade desse artigo um cliente terá
que desembolsar R$ 42,00, o seu preço de tabela é
(A) R$ 20,00
(B) R$ 24,50
(C) R$ 30,00
(D) R$ 32,50
(E) R$ 35,00
SOLUÇÃO
1. Se o cliente desembolsou R$ 42,OO após um desconto de 25% sobre o preço fixado, o preço fixado seria 42/(1-0.25) = R$56,00
2. O lucro do comerciante será L = 42 - 0.8 *P_tab
3. Uma vez que o lucro deve ser 40% do preço fixado, devemos ter L = 0.4 * 56 =R$ 22,40
4. Se L = 22.4 $ então 42 - 0.8*P_tab = 22.4, pelo que P_tab = (42-22.4)/0.8 = R$ 24,50
2. O lucro do comerciante será L = 42 - 0.8 *P_tab
3. Uma vez que o lucro deve ser 40% do preço fixado, devemos ter L = 0.4 * 56 =R$ 22,40
4. Se L = 22.4 $ então 42 - 0.8*P_tab = 22.4, pelo que P_tab = (42-22.4)/0.8 = R$ 24,50
ALTERNATIVA: B
segunda-feira, 14 de outubro de 2013
Prova CEF/2012 Resolvida e Comentada
Questão 6.
Um projeto de investimento, cujo aporte de capital inicial é
de R$ 20.000,00, irá gerar, após um período, retorno de R$ 35.000,00. A Taxa
Interna de Retorno (TIR) desse investimento é
(A) 275%
(B) 175%
(C) 34%
(D) 75%
(E) 43%
(B) 175%
(C) 34%
(D) 75%
(E) 43%
Resolução: Aqui, a TIR será simplesmente a taxa de
juros desta aplicação. Os juros da aplicação foram de R$ 15.000,00. Assim,
temos:
i = juros / capital = 15.000 / 20.000 = 0,75 = 75%. Letra
D. Questão de barbada.
Questão 7.
Nas operações de empréstimo, uma financeira cobra taxa
efetiva de juros, no regime de capitalização composta, de 10,25% ao ano. Isso
equivale a cobrar juros com taxa anual e capitalização semestral de
(A) 10,51%
(B) 10,25%
(C) 5%
(D) 10%
(E) 5,51%
(B) 10,25%
(C) 5%
(D) 10%
(E) 5,51%
Resolução: Como o examinador pede uma taxa de
capitalização mensal, temos de saber, antes de tudo, a taxa efetiva semestral,
bastando para isso tirar a raiz quadrada de 1,1025 = 1,05, ou seja, teremos uma
taxa efetiva semestral de 5%. Agora, teremos de transformar esta taxa para
nominal anual. Como um ano possui dois semestre, multiplicamos a taxa por 2.
Assim, teremos 10% ao ano, capitalizados semestralmente. Letra D.
Outra fácil.
Questão 8.
Um imóvel de 100 mil reais é financiado em 360 prestações
mensais, a uma taxa de juros de 1% ao mês, pelo Sistema de Amortização Francês
(Tabela Price), gerando uma prestação de R$ 1.028,61. Reduzindo-se o prazo do
financiamento para 240 prestações, o valor de cada prestação é, em reais,
aproximadamente,
Dado: (1,01)^(−120) = 0,3
(A) 2.127,00
(B) 1.714,00
(C) 1.099,00
(D) 1.428,00
(E) 1.371,00
(B) 1.714,00
(C) 1.099,00
(D) 1.428,00
(E) 1.371,00
Resolução: Precisamos simplesmente calcular o valor
da prestação, reduzindo-se o prazo para 240 meses. Assim como nas provas da
Cespe, é dado um fator elevado em um expoente negativo. O examinador tenta
levar o candidato inexperiente ao erro, contudo, basta sabermos um pouco de
exponenciais, que fugimos dessa fria:
Basta transformarmos para:
(1,01)^(−120) = 0,3; então: (1,01)^(120) = 10/3;
sabemos que (1,01)^(240) = (1,01)^(120) . (1,01)^(120) =
10/3 x 10/3 = 100/9 = 11,11
R = P . [(1+i)^n . i] / [(1+i)^n - 1], onde:
P = valor do financiamento de R$ 100.000,00;
R = valor da nova prestação, pedida na questão;
n = prazo de 240 meses
i = taxa efetiva mensal de juros de 1%
R = 100.000 . [(1,01)^240 . 0,01] / [(1,01)^240
- 1] =100.000 . [11,11 . 0,01] / [11,11 - 1] = 1.099,00;letra C.
Questão 9.
O setor financeiro de uma empresa, que tem taxa mínima de
atratividade de 10% ao ano, avalia duas alternativas: montar um laboratório
fotográfico ou terceirizar o serviço de fotografias. Para a opção de montar o
laboratório fotográfico, o investimento inicial, os custos pagos ao final de
cada ano, o tempo de utilização do laboratório e a informação adicional do
valor presente liquido (VPL) do fluxo de caixa estão apresentados no quadro a
seguir.
Investimento inicial R$ 100.301,65
Custo operacional anual R$ 7.000,00
Custo de manutenção anual R$ 3.000,00
Valor residual zero
Tempo de utilização 4 anos
VPL R$ 132.000,30
Custo operacional anual R$ 7.000,00
Custo de manutenção anual R$ 3.000,00
Valor residual zero
Tempo de utilização 4 anos
VPL R$ 132.000,30
No caso de terceirizar o serviço, o custo de manutenção fica
por conta da empresa contratada. É mais atraente terceirizar se, e somente se,
o custo operacional anual dessa opção, em reais, for, no máximo, de
Dado: (1,10)^(−4) = 0,68 … temos, então que 1,10^4 =
100/68 = 1,47
(A) 11.760,00
(B) 22.060,40
(C) 42.240,10
(D) 33.000,08
(E) 41.250,10
(B) 22.060,40
(C) 42.240,10
(D) 33.000,08
(E) 41.250,10
Resolução: Basta considerarmos o VPL dado de R$
132.000,30 como valor presente do fluxo de caixa para o custo da terceirização,
considerando 4 anos de utilização. Assim, temos:
R = P . [(1+i)^n . i] / [(1+i)^n - 1] = 130.000
R = 132.000,30 . [(1,10)^4 . 0,10] / [(1,10)^4 -
1] =132.000,30 . [1,47 . 0,10] / [1,47 - 1] = 41.285,20, sendo o
valor mais próximo, letra E.
Questão 10.
O montante gerado por uma instituição financeira, em uma
aplicação no regime de juros compostos, é R$ 5.000,00, em
10 meses, ou R$ 5.202,00, em 1 ano. Se a taxa de juros é constante, o valor aplicado é, em reais, de, aproximadamente,
10 meses, ou R$ 5.202,00, em 1 ano. Se a taxa de juros é constante, o valor aplicado é, em reais, de, aproximadamente,
(A) 4.100
(B) 3.950
(C) 1.950
(D) 3.400
(E) 3.100
(B) 3.950
(C) 1.950
(D) 3.400
(E) 3.100
Resolução: Primeiramente, precisamos descobrir a taxa
de juros compostos da aplicação. Consideramos, para isso, o capital de 5.000,00
que se torna em 2 meses o valor de 5.202,00. Utilizando a fórmula de juros
compostos, e isolando o termo i, chegamos a uma taxa mensal de 2%. Com esta
taxa, trazemos a valor presente o montante de 5.000,00, em 10 meses. Bastando,
para isso, multiplicar 5.000 pelo fator dado na tabela:
1,02 ^ (-10) = 0,82. Assim, 5.000 x 0,82 = 4.100,00, que é o
capital inicialmente aplicado. Letra A.
sexta-feira, 13 de setembro de 2013
quarta-feira, 11 de setembro de 2013
quinta-feira, 22 de agosto de 2013
terça-feira, 23 de julho de 2013
quinta-feira, 18 de julho de 2013
QUESTÃO RESOLVIDA
Uma
loja vende certo artigo por 15 reais. Em uma promoção, o preço de venda desse
artigo foi baixado para x re-ais e isso fez que todas as n unidades em estoque,
que não eram mais do que 30, fossem vendidas. Se com a venda das n unidades foi
arrecado o total de 253 reais e sendo x um número inteiro, então n-x é igual a:
a)6
b)8
c)9
d)12
e)14
Do
enunciado da questão, obtém-se a seguinte equação:
N . x = 253
Em
que N é quantidade vendida e X é o valor
vendido. Fatorando a equa-ção acima, temos que 253=23x11. Como, os valores de N
e X são números inteiros positivos, e sabendo que é menor que 15, pois o valor
inicial era 15 reais e foi reduzido para x
N=
23
X
= 11
Portanto
n – x = 12, LETRA D
terça-feira, 9 de julho de 2013
terça-feira, 18 de junho de 2013
QUESTAO RESOLVIDA
Uma loja de eletrodomésticos anunciou a seguinte promoção: "Pague em 15 prestações iguais, sem juros, ou, à vista, com 10% de desconto". Considere um fogão que pode ser pago em 15 prestações de p reais. O valor do desconto para quem comprar o mesmo fogão e optar pelo pagamento à vista será equivalente a qual fração de p?
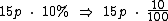
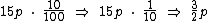
 O valor do desconto será equivalente a 3/2p.
O valor do desconto será equivalente a 3/2p.
A resolução desta questão requer um conhecimento básico sobre porcentagens e sobre a simplificação de frações.
Pago a prazo o fogão custará 15p reais, o desconto de 10% equivale a:
Agora basta simplificarmos a expressão:
Logo:
 O valor do desconto será equivalente a 3/2p.
O valor do desconto será equivalente a 3/2p.quarta-feira, 17 de abril de 2013
QUESTÃO CESPE
Cespe -( Previc - 2011 )
Considerando que, em uma concessionária de veículos, tenha sido
verificado que a probabilidade de um comprador adquirir um carro
de cor metálica é 1,8 vez maior que a de adquirir um carro de cor
sólida e sabendo que, em determinado período, dois carros foram
comprados, nessa concessionária, de forma independente, julgue os
itens a seguir.
1 - A probabilidade de que ao menos um dos dois carros
comprados seja de cor sólida é igual a . 460
784
2 - A probabilidade de que os dois carros comprados sejam de cor
metálica é 3,24 vezes maior que a probabilidade de que eles
sejam de cor sólida.
3 - A probabilidade de que somente um dos dois carros comprados
seja de cor metálica é superior a 50%.
Considerando que, em uma concessionária de veículos, tenha sido
verificado que a probabilidade de um comprador adquirir um carro
de cor metálica é 1,8 vez maior que a de adquirir um carro de cor
sólida e sabendo que, em determinado período, dois carros foram
comprados, nessa concessionária, de forma independente, julgue os
itens a seguir.
1 - A probabilidade de que ao menos um dos dois carros
comprados seja de cor sólida é igual a . 460
784
2 - A probabilidade de que os dois carros comprados sejam de cor
metálica é 3,24 vezes maior que a probabilidade de que eles
sejam de cor sólida.
3 - A probabilidade de que somente um dos dois carros comprados
seja de cor metálica é superior a 50%.
CM = 1,8CS
CM + CS = 1
1,8CS + CS = 1
2,8CS = 1
CS = 1/2,8 = 10/28
.
CM = 18/28
1 - A probabilidade de que ao menos um dos dois carros comprados seja de cor sólida é igual a . 460/784
.
CS*CM + CM*CS + CS*CS
10/28*18/28 + 18/28 *10/28 + 10/28*10/28 = 180/784 + 180/784 + 100/784 = 460/784
.
Ou
1 – CM*CM
1 – 18/28*18/28 = 1 – 324/784 = (784 – 324)/784 = 460/784
Item Certo
2 - A probabilidade de que os dois carros comprados sejam de cor metálica é 3,24 vezes maior que a probabilidade de que eles sejam de cor sólida.
.
CS = 10/28 * 10/28 = 100/784
CM = 18/28 * 18/28 = 324/784
.
P = (324/784) / (100/784) = 324/100 = 3,24 vezes maior
Item certo
3 - A probabilidade de que somente um dos dois carros comprados seja de cor metálica é superior a 50%.
.
pode ser: CS*CM + CM*CS
10/28*18/28 + 18/28 *10/28 = = 180/784 + 180/784 = 360/784 = 0,45
Item errado.
.
Gabarito: 1 C 2 C 3 E
CM + CS = 1
1,8CS + CS = 1
2,8CS = 1
CS = 1/2,8 = 10/28
.
CM = 18/28
1 - A probabilidade de que ao menos um dos dois carros comprados seja de cor sólida é igual a . 460/784
.
CS*CM + CM*CS + CS*CS
10/28*18/28 + 18/28 *10/28 + 10/28*10/28 = 180/784 + 180/784 + 100/784 = 460/784
.
Ou
1 – CM*CM
1 – 18/28*18/28 = 1 – 324/784 = (784 – 324)/784 = 460/784
Item Certo
2 - A probabilidade de que os dois carros comprados sejam de cor metálica é 3,24 vezes maior que a probabilidade de que eles sejam de cor sólida.
.
CS = 10/28 * 10/28 = 100/784
CM = 18/28 * 18/28 = 324/784
.
P = (324/784) / (100/784) = 324/100 = 3,24 vezes maior
Item certo
3 - A probabilidade de que somente um dos dois carros comprados seja de cor metálica é superior a 50%.
.
pode ser: CS*CM + CM*CS
10/28*18/28 + 18/28 *10/28 = = 180/784 + 180/784 = 360/784 = 0,45
Item errado.
.
Gabarito: 1 C 2 C 3 E
sábado, 13 de abril de 2013
QUESTÃO RESOLVIDA
Duas pessoas A e B disputam 200 partidas de um jogo. Sempre que A vence uma partida, recebe R$6,00 de B, e sempre que B vence, recebe R$10,00 de A. o menor numero de partidas que A deve ganhar para ter lucro é?
a 168
b 132
c 141
d 157
e 126
SOLUÇÃO
Iniciamos fazendo x o número de vitórias de A.
Então o número de derrotas de A é menor ou igual a 200-x. Como não sabemos se há empates, e quanto custaria o empate, o valor deste não deve ser pior do que a derrota. Então na pior das hipóteses, A perde todas as partidas que ele não vence
O lucro de A é o que ele ganha menos o que ele perde.
L >= 6.x - 10(200-x)
L >= 6.x - 2000 + 10.x
L >= 16.x - 2000
Para houver algum lucro, L >=0
L >= 16.x - 2000 >= 0
16x >= 2000
x >= 125
Então, se A vencer 125 partidas, fica tudo na mesma, mas se ele vencer 126 partidas ou mais, terá lucro.
Alternativa E
a 168
b 132
c 141
d 157
e 126
SOLUÇÃO
Iniciamos fazendo x o número de vitórias de A.
Então o número de derrotas de A é menor ou igual a 200-x. Como não sabemos se há empates, e quanto custaria o empate, o valor deste não deve ser pior do que a derrota. Então na pior das hipóteses, A perde todas as partidas que ele não vence
O lucro de A é o que ele ganha menos o que ele perde.
L >= 6.x - 10(200-x)
L >= 6.x - 2000 + 10.x
L >= 16.x - 2000
Para houver algum lucro, L >=0
L >= 16.x - 2000 >= 0
16x >= 2000
x >= 125
Então, se A vencer 125 partidas, fica tudo na mesma, mas se ele vencer 126 partidas ou mais, terá lucro.
Alternativa E
sábado, 6 de abril de 2013
QUESTÃO RESOLVIDA
Sejam a e b as raízes da equação x²- 7x + m=3. Se 1/a + 1/b = 1 , então valor de m é:
a]10
b] 4
c] -4
d] -10
e] 1
SOLUÇÃO
x² -7x +m-3
A soma dos inversos das raízes é sempre igual à -b/c, para as equações do segundo grau.
1/a + 1/b = 1 = -b/c
-b/c = 1
7/(m-3) = 1
m-3 = 7
m = 10
Opção A
a]10
b] 4
c] -4
d] -10
e] 1
SOLUÇÃO
x² -7x +m-3
A soma dos inversos das raízes é sempre igual à -b/c, para as equações do segundo grau.
1/a + 1/b = 1 = -b/c
-b/c = 1
7/(m-3) = 1
m-3 = 7
m = 10
Opção A
sexta-feira, 22 de março de 2013
QUESTÕES RESOLVIDAS RAZÃO E PROPORÇÃO
3. (PM-ES 2013) O Batalhão de Polícia
Militar Ambiental da PMES contava com um efetivo de 30 policiais em 1987. Em
2012, contava com um efetivo de 180 policiais. Supondo linear a taxa de crescimento
do efetivo de policiais no Batalhão de Polícia Militar Ambiental nos últimos 25
anos, e que a mesma taxa de crescimento permanecerá constante nos próximos
cinco anos, o número total de policiais no Batalhão de Polícia Militar
Ambiental, ao final desses cinco anos, será de:
A) 200
B) 210
C) 220
D) 230
E) 240
Note que o efetivo teve um aumento de 150 policiais em 25 anos, ou seja,
150/25 = 6 por ano.
Logo, nos próximos 5
anos irá aumentar em 30 policiais. 180 + 30 = 210
2. (CESPE - Carteiro Correios 2011) Em 01/01/2011, os
Correios lançaram selo comemorativo de data histórica, com tiragem de 900.000
unidades. Do dia 1 ao dia 10 de janeiro, foram vendidas 210.630 unidades desses
selos, das quais 1.958 foram vendidas apenas no dia 4, primeiro dia de
comercialização do selo via Internet. O prazo de comercialização desse selo
pelos Correios vigorará até 31/12/2014.
Com base nas informações do texto acima e considerando-se que o ritmo de
venda do selo tenha sido mantido ao longo do mês de janeiro de 2011, é correto
afirmar que a quantidade de selos vendidos, em milhares de unidades, até o dia
30 do referido mês, foi:
A. superior a 640.
B. inferior a 610.
C. superior a 610 e inferior a 620.
D. superior a 620 e inferior a 630.
E. superior a 630 e inferior a 640.
Note que o texto apresenta várias informações, a maioria irrelevante
para nossa questão.
Como nos 10 primeiros
dias foram comercializados 210.630 selos e o ritmo das vendas em janeiro se
manteve, temos que até o dia 30 de janeiro serão comercializados 3 x 210630 =
631.890
1. (CESPE - Carteiro Correios 2011) Se, em 2010, o
projeto Papai Noel dos Correios contou com 22.435 voluntários, e se foi mantida
a mesma proporção de voluntários externos e internos verificada em 2009, então
a quantidade de voluntários internos em 2010 foi:
A. superior a 19.050 e inferior a 19.100.
B. superior a 19.100 e inferior a 19.150.
C. superior a 19.150.
D. inferior a 19.000.
E. superior a 19.000 e inferior a 19.050.
Total de voluntários em 2009: 3818 + 669 = 4487
Proporção de voluntáros internos em 2009: 3818/4487
Como a proporção foi a mesma de 2009 e em 2010 foram 22435 voluntários:
x = 3818 4487x = 3818.22435
22435 4487
4487x = 85656830
x = 85656830 / 4487 = 19090
quarta-feira, 13 de março de 2013
QUESTÃO RESOLVIDA
Um carpinteiro recebeu a incumbência de cortar 40 toras de madeira de 8 metros cada uma e 60 toras da mesma madeira de 6 metros cada, em toras de mesmo comprimento, sendo o comprimento o maior possível. Quantas toras de madeira serão obtidas?
SOLUÇÃO:
1º calculamos o MDC dos comprimentos dados (8m e 6m): é 2m, que será o tamanho das toras.
2º dividimos 8m por 2m, obtendo 4 toras por tora inicial. 4 x 40 = 160 novas toras.
3º dividimos 6m por 2m, obtendo 3 toras por tora inicial. 3 x 60 = 180 novas toras.
4º somamos tudo: 160 + 180 = 340 toras de 2m cada.
sábado, 2 de fevereiro de 2013
quarta-feira, 30 de janeiro de 2013
DIVISORES DE UM NUMERO
Divisores de um Número
Divisores de um Número
Definimos divisores de um número n, como sendo o conjunto numérico formado por todos os números que o dividem exatamente.
Vejamos o 12 por exemplo:

Somente os quocientes 1, 2, 3, 4, 6 e 12 o dividem exatamente, já o quociente 5 não o divide exatamente. Sendo assim, o conjunto dos
divisores de 12 é :
D(12) = { 1, 2, 3, 4, 6 e 12 } , da mesma forma teríamos :
D(4) = { 1, 2, e 4 } D(10) = { 1, 2, 5 e 10 } D(18) = { 1, 2, 3, 6, 9 e 18 }
D(24) = { 1, 2, 3, 4, 6, 8, 12 e 24 } D(40) = { 1, 2, 4, 5, 8, 10, 20 e 40 }
Com isso percebemos que :
O conjunto dos divisores de um número é um conjunto finito, já que possui uma quantidade limitada de elementos.
O conjunto dos divisores da unidade é um conjunto unitário formado pelo elemento 1 D(1) = { 1 }
O conjunto dos divisores do ZERO é um conjunto infinito formado por todos os números naturais diferentes de 0.
D(0) = { 1 , 2, 3, 4 ,5 , 6, 7, 8 , 9, 10, 11, 12 , 13, ....}
Lembremos que IN - { 0 } = { 1 , 2, 3, 4 ,5 , 6, 7, 8 , 9, 10, 11, 12 , 13, ....} .
O conjunto dos divisores de um número diferente de 1 ou 0 tem no mínimo dois divisores, ele mesmo e a unidade. Assim :
D(7) = { 1, 7 } D(9) = { 1, 3 , 9 } D(11) = { 1, 11 } D(7) = { 1, 3, 5, 15 }
E com isso percebemos que a unidade é divisor de todo e qualquer número.
Observação Importante: Alguns autores e alguns concursos, como o Colégio Naval, estendem a definição de divisores de um número
para o conjunto dos números inteiros, e com isso teremos divisores positivos e negativos. Assim :
D(12) = { -12, - 6, - 4, -3, -2, 1, 1, 2, 3, 4, 6, 12 } , mas só devemos considerar dessa forma se isso ficar bem claro numa questão.
Números Primos
Números Primos são aqueles que possuem somente dois divisores, ele mesmo e a unidade. Alguns números primos :
D(2) = { 1, 2 } D(5) = { 1, 5 } D(7) = { 1, 7 } D(19) = { 1, 19 }
Com isso percebemos que :
O 2 é o único número par que é primo.
A unidade não é um número primo pois possui apenas 1 divisor D(1) = { 1 }
O ZERO não é um número primo pois possui uma infinidade de divisores D(0) = { 1 , 2, 3, 4 ,5 , 6, 7, 8 , 9, 10, 11, 12 , 13, ....}
O conjunto dos números primos é um conjunto infinito Primos = { 2, 3, 5, 7, 11, 13, 17, 19, 23, ....}
Números Compostos
Números Compostos são aqueles que possuem uma quantidade finita de 3 ou mais divisores . Alguns números compostos :
D(4) = { 1, 2, 4 } D(8) = { 1, 4, 8 } D(24) = { 1,2, 3, 4, 6, 8, 12, 24 }
D(42) = { 1, 2, 3, 6, 7, 14, 21, 42 } D(50) = { 1,2, 5, 10, 25, 50 }
Com isso percebemos que :
Com exceção do 2, todos os demais números pares são compostos.
A unidade não é um número composto pois possui apenas 1 divisor D(1) = { 1 }
O ZERO não é um número composto pois possui uma infinidade de divisores D(0) = { 1 , 2, 3, 4 ,5 , 6, 7, 8 , 9, 10, 11, 12 , 13, ....}
O conjunto dos números compostos é um conjunto infinito Compostos = { 4, 6, 8, 9, 10, 12, 14, 15, 18, ....}
E dessa forma podemos classificar os números em quatro categorias :
Um número N poderá ser o 0, a unidade, um número primo ou um número composto.
Reconhecimento de um Número Primo
Um número terminado em 1, 3, 7 e 9 será primo quando dividido sucessivamente pela listagem crescente dos números primos menores
que ele, gerar divisões inexatas e quando o quociente da divisão se tornar menor ou igual a ele .
Verifiquemos, por exemplo, se 173 é primo : Vamos dividi-lo pelos primos menores que ele a começar pelo 2.

Notemos que gradativamente os quocientes obtidos vão diminuindo e cada divisão se mantém inexata, até que o quociente 13 e o
divisor tornam-se iguais. Com isso podemos afirmar que 173 é um número primo.
Verifiquemos, agora, se 187 é primo :
Vamos dividi-lo pelos primos menores que ele a começar pelo 2.

Notemos que gradativamente os quocientes obtidos vão diminuindo e cada divisão se mantém inexata, até que ao dividirmos 187
por 11 o resto torna-se 0. Com isso podemos afirmar que 187 não é um número primo, já que ele é divisível por 11 e também por 17 .
Somente poderá ser primo um número terminado em 1, 3 , 7 ou 9
Listagem dos Números Primos Menores que 1 000
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 87 89 97 101 103 107 109 113 119
121 123 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479
487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683
691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911
919 929 937 941 947 953 967 971 977 983 991 997
Decomposição de um Número em Fatores Primos
Por diversas ocasiões precisamos decompor um número num produto de fatores primos. Assim :
20 = 4 x 5, e usando apenas fatores primos => 20 = 2 x 2 x 5 ou 22 x 5
60 = 4 x 15, e usando apenas fatores primos => 60 = 2 x 3 x 5 ou 22 x 3 x 5
7800 = 8 x 3 x 25 x 13, e usando apenas fatores primos => 23 x 3 x 52 x 13
2772 = 4 x 9 x 7 x 11, e usando apenas fatores primos => 22 x 32 x 7 x 11
Método prático para a decomposição de um número em fatores primos
Escrevemos o Número
A sua direita traçamos uma linha vertical
Vamos dividí-lo sucessivamente pelos números primos a partir do 2
Enquanto a divisão for possível continuaremos a divisão
Não sendo mais possível passamos para o próximo número primo
E assim faremos até que cheguemos a unidade.
Vejamos alguns Exemplos
Decomponha 120 em
fatores primos Decomponha 312 em
fatores primos Decomponha 495 em
fatores primos Decomponha 900 em
fatores primos
120 = 23 X 3 X 5 312 = 23 X 3 X 13 495 = 32 X 5 X 11 900 = 22 X 32 X 5




Cálculo dos Divisores de um Número
Escrevemos o Número
À sua direita traçamos uma linha vertical
Vamos decompô-lo em fatores primos
Feito isso traçamos a direita dos fatores primos uma nova linha vertical
A direita dessa linha e acima do menor número primo encontrado lançamos a unidade
Multiplicamos o menor fator primo encontrado por todos os números que se encontram acima dele e escrevemos os resultados à
direita do traço vertical e na mesma linha do fator primo
Se o fator primo for o mesmo do anterior multiplicaremos esse fator apenas pela linha de cima.
Se o fator primo for diferente do anterior começaremos nossa multiplicação pela unidade e continuaremos por todos os números
acima dele
E assim faremos até chegarmos ao número original que é o maior divisor possível.
Todos os números encontrados a direita do segundo traço vertical serão os divisores do número solicitado.
Vejamos alguns Exemplos
Exemplo 1 - Quais são os divisores de 120 Exemplo 2 - Quais são os divisores de 158
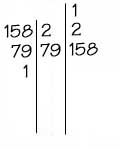

Os divisores de 120 são :
1 - 2 - 3 - 4 - 5 - 6 - 8 - 10 - 12 - 15 - 18 - 20 - 30 - 40 - 60 - 120 Os divisores de 158 são :
1 - 2 - 79 - 158
Exemplo 3 - Quais são os divisores de 200 Exemplo 4 - Quais são os divisores de 396


Os divisores de 200 são :
1 - 2 - 4 - 5 - 8 - 10 - 20 - 25 - 40 - 50 - 100 - 200 Os divisores de 396 são :
1 - 2 - 3 - 4 - 6 - 9 - 11 - 12 - 18 - 22 - 33 - 36 - 44 - 66 - 99 - 132 - 198 - 396
Cálculo da Quantidade de Divisores de um Número
Em muitas situações precisamos conhecer apenas a quantidade de divisores de um número sem conhecermos exatamente quais são
eles :
E para tal utilizaremos a fórmula : ( Mais tarde a deduziremos )
A quantidade de divisores de um número é dado pelo produto entre os
consecutivos dos expoentes de todos os seus fatores primos.
Exemplo 1 - Quantos são os divisores de 60
Decomposição em fatores primos 60 = 22 x 3 x 5
Expoentes dos fatores primos 2 , 1 e 1
Consecutivos dos Expoentes 2 + 1 = 3 , 1 + 1 = 2 e 1 + 1 = 2
Produto entre os consecutivos 3 x 2 x 2 = 12
O número 60 possui 12 divisores
Exemplo 2 - Quantos são os divisores de 720
Decomposição em fatores primos 720 = 24 x 32 x 5
Expoentes dos fatores primos 4 , 2 e 1
Consecutivos dos Expoentes 4 + 1 = 5 , 2 + 1 = 3 e 1 + 1 = 2
Produto entre os consecutivos 5 x 3 x 2 = 30
O número 720 possui 30 divisores
Cálculo da Quantidade dos Divisores Ímpares de um Número
Em muitas situações precisamos conhecer apenas a quantidade de divisores ímpares de um número sem conhecermos exatamente
quais são eles :
E para tal utilizaremos a fórmula : ( Mais tarde a deduziremos )
A quantidade de divisores ímpares de um número é dado, exclusivamente, pelo
produto entre os consecutivos dos expoentes de seus fatores primos ímpares..
Exemplo 1 - Quantos são os divisores ímpares de 540
Decomposição em fatores primos 540 = 22 X 33 X 5
Expoentes dos Fatores primos ímpares 3 e 1
Consecutivos dos Expoentes 3 + 1 = 4 e 1 + 1
Produto entre os consecutivos 4 x 2 = 8
O Número 540 possui 8 divisores ímpares
Exemplo 2 - Quantos são os divisores ímpares de 3 150
Decomposição em fatores primos 3 150 = 2 x 33 x 5 x 7
Expoentes dos Fatores primos ímpares 3, 1 e 1
Consecutivos dos Expoentes 3 + 1 = 4 , 1 + 1 = 2 e 1 + 1= 2
Produto entre os consecutivos 4 x 2 x 2 = 16
O Número 3 150 possui 16 divisores ímpares
Cálculo da Quantidade dos Divisores Pares de um Número
Lembremos que somente um número par terá divisores pares
A quantidade de divisores pares de um número par é dado pelo produto entre o expoente do fator primo 2 e os consecutivos dos expoentes dos demais fatores primos ..
Exemplo 1 - Quantos são os divisores pares de 360
Decomposição em fatores primos 360 = 23 X 32 X 5
Expoente do fator primo 2 3
Expoentes dos Fatores primos ímpares 2 e 1
Consecutivos dos Expoentes 2 + 1 = 3 e 1 + 1 = 2
Produto entre 3 ( expoente do fator primo 2 ) e os consecutivos dos demais fatores primos 3 x 3 x 2 = 18
O Número 360 possui 18 divisores pares
Exemplo 2 - Quantos são os divisores pares de 420
Decomposição em fatores primos 840 = 22 X 3 X 5 X 7
Expoente do fator primo 2 2
Expoentes dos Fatores primos ímpares 1, 1 e 1
Consecutivos dos Expoentes 1 + 1 = 2 , 1 + 1 = 2 e 1 + 1 = 2
Produto entre 2 ( expoente do fator primo 2 ) e os consecutivos dos demais fatores primos 2 x 2 x 2 x 2 = 16
O Número 840 possui 16 divisores pares
Cálculo da quantidade dos múltiplos de um número p dentre os divisores de um número N
OBS => Esse cálculo somente terá sentido se p for divisor de N
1º Caso : O número p é um fator primo de N
A quantidade de divisores múltiplos de um número p é dado pelo produto entre o expoente do fator primo p e os consecutivos dos expoentes dos demais fatores primos..
Exemplo 1 - Quantos divisores de 720 são múltiplos de 3
Decomposição em fatores primos 720 = 24 x 32 x 5
Expoente do fator primo 3 2
Expoentes dos demais fatores primos 4 e 1
Consecutivos dos Expoentes 4 + 1 = 5 , 1 + 1 = 2
Produto entre 2 ( expoente do fator primo 3 ) e os consecutivos dos demais fatores primos 2 x 5 x 2 = 20
O Número 720 possui 20 divisores múltiplos de 3
Exemplo 2 - Quantos divisores de 2 880 são múltiplos de 5
Decomposição em fatores primos 2 880 = 26 x 32 x 5
Expoente do fator primo 5 1
Expoentes dos demais fatores primos 6 e 2
Consecutivos dos Expoentes 6 + 1 = 7 , 2 + 1 = 3
Produto entre 1 ( expoente do fator primo 5 ) e os consecutivos dos demais fatores primos 1 x 7 x 3 = 21
O número 2 880 possui 21 divisores múltiplos de 5
2º Caso : O número p é composto e é um produto de fatores primos de N
A quantidade de divisores múltiplos de um número composto p é dado pelo
produto entre os consecutivos dos expoentes dos fatores primos restantes..
Exemplo 1 - Quantos divisores de 720 são múltiplos de 12
Decomposição em fatores primos 720 = 24 x 32 x 5
Isolemos o produto 12 ( 22 X 3 ) X 22 X 3 X 5
Expoentes dos demais fatores primos 2, 1 e 1
Consecutivos dos Expoentes 2 + 1, 1 + 1 e 1 + 1
Produto entre os consecutivos 3 X 2 X 2= 12
O número 720 possui 12 divisores múltiplos de 12
Exemplo 2 - Quantos divisores de 1 440 são múltiplos de 40
Decomposição em fatores primos 1 440 = 25 x 32 x 5
Isolemos o produto 40 ( 23 X 5 ) X 22 X 32
Expoentes dos demais fatores primos 2 e 2
Consecutivos dos Expoentes 2 + 1 e 2 + 1
Produto entre os consecutivos 2 X 2= 4
O número 1 440 possui apenas 4 divisores múltiplos de 40
Uma regra prática e bastante útil nesse caso seria a de dividirmos o número N pelo número p e a quantidade de divisores desse quociente nos dará a quantidade de múltiplos de p dentre os divisores de N.
Exercícios Propostos
I - Quais são os divisores de :
01) 20 02) 45 03) 72 04) 128
05) 400 06) 560 07) 1 040 08) 1 200
II - Calcule o produto entre os divisores positivos de :
09) 36 10) 48 11) 60 12) 144
III - Calcule o produto entre os divisores inteiros de :
13) 30 14) 54 15) 105 16) 108
IV - Verifique se são primos os números :
17) 237 18) 267 19) 343 20) 433
21) 851 22) 953 23) 1 049
24) Mostre que a soma dos algarismos de um número primo não pode ser 15 e nem 21.
VI - Determine o valor de x para que os números abaixo sejam primos
25) 1x3 26) 32x 27) 54x 28) 63x5
29) Podemos afirmar que não existem números consecutivos primos ?
30) O consecutivo de um número primo é sempre um número ....... .
31) Podemos afirmar que todo número primo com mais de um algarismo é ímpar ?
VII - Decomponha em fatores primos :
32) 24 33) 38 34) 56 35) 96 36) 180
37) 240 38) 320 39) 539 40) 936 41) 1024
42) 1440 43) 3850 44) 3960 45) 4500
VII - Decomponha em fatores primos as multiplicações :
46) 24 x 30 47) 38 x 60 x 72 48) 32 x 40 x 108
49) 22 x 33 x 44 x 77 50) 122 x 203 x 212 51) 15 n x 18 n x 28 n
VIII - Quantos são os divisores de :
52) 72 53) 96 54) 360 55) 450 56) 600
57) 740 58) 840 59) 1 120 60) 1 560 61) 1 800
IX - Quantos são os divisores pares de :
62) 36 63) 60 64) 96 65) 420 66) 660
67) 720 68) 900 69) 1 200 70) 1 440 71) 2 000
X - Quantos são os divisores ímpares de :
72) 54 73) 234 74) 275 75) 1 428 76) 7 425
XI - Determine o valor de n para que os números tenham :
77) 22 x 3n x 5 - 18 divisores 78) 23 x 32 x 7n - 36 divisores 79) 24 x 5n x 11n - 45 divisores
80) 123 x 52 x 13n - 168 divisores 81) 24n x 72 x 23 - 126 divisores 82) 123 x 52 x 13n - 168 divisores
XII - Qual o menor número da forma 2a X 3b que possui :
83) 12 84) 20 85) 36 86) 40
XIII - Qual o menor número da forma 2a X 3b X 5c que possui :
87) 18 88) 24 89) 60
XIV - Dentre os divisores de 60, quantos são múltiplos de :
90) 6 91) 10 92) 12 93) 18 94) 20
XV - Dentre os divisores de 120, quantos são múltiplos de :
95) 8 96) 10 97) 12 98) 15 99) 30
XVI - Dentre os divisores de 300, quantos são múltiplos de :
100) 4 101) 6 102) 12 103) 18 104) 60
105) Dentre os divisores de 180, quantos não terminam em 0 ?
106) Dentre os divisores de 90, quantos terminam em cinco ?
Questões de Concurso
107)( CEFETQ 1992 - Discursiva ) Na decomposição em fatores primos de um número natural N, encontramos o seguinte resultado:
3x . 3y . 5z . Sabendo que possui 105 divisores, calcule o valor de x + y + z.
108) ( CEFET 2000 - Discursiva ) Seja N = 2 x 302 , qual o número de divisores de N que são também múltiplos de 15 ?
109) ( Colégio Naval - 1982 ) Seja N = 24 x 35 x 56 . O número de divisores de N que são múltiplos de 10, é
A) 24 B) 35 C) 120 D) 144 E) 210
110) ( Colégio Naval - 1984 ) Seja o número , o número de divisores positivos de N é :
A) 6 B) 15 C) 2 D) 13 E) 4
111)( CEFET 1996 ) A soma dos valores absolutos dos algarismos de um número superior a 1010 e inferior a 2010 e ao mesmo tempo
múltiplo de 7, 11 e 13 é:
A) 2 B) 5 C) 15 D) 11 E) 22
112) ( EPCAR 2001 ) Sobre o menor número natural n de 4 algarismos, divisível por 3, tal que o algarismo das dezenas é a metade do
algarismo das unidades e igual ao dobro do algarismo das unidades de milhar. É correto afirmar que
A) n + 1 é divisível por 7 B) n está entre 2000 e 3009
C) n + 2 é múltiplo de 10 D) n apresenta 12 divisores positivos
113) ( Colégio Naval - 1991 ) O produto de todos os divisores inteiros de 144 é :
A) - 230 X 315 B) 230 X 315 C) - 260 X 330 D) 260 X 330 E) - 630
114) ( CEFET 1995 - Discursiva ) Determine a soma dos valores absolutos de um número que é superior a 500, inferior a 1000 e é, ao
mesmo tempo, múltiplo de 3, 11 e 13 .
115) ( Colégio Naval - 1990 ) Os números da forma 4k 2 + 50 + 4k 2 + 51 + 4k 2 + 52 + 4k 2 + 53 são sempre múltiplos de:
A) 17 B) 19 C) 23 D) 29 E) 31
116) ( Colégio Naval - 1996 ) Os números naturais M e N são formados por dois algarismos não nulos. Se os algarismos de M são os
mesmos algarismos de N, na ordem inversa, então M + N é necessariamente múltiplo de :
A) 2 B) 3 C) 5 D) 7 E) 11
117) ( Colégio Naval - 2001 ) Se a e b são números naturais e 2a + b é divisível por 13, então um número múltiplo de 13 será :
A) 91a + b B) 92a + b C) 93a + b D) 94a + b E) 95a + b
domingo, 27 de janeiro de 2013
QUESTÃO RESOLVIDA
Eu tenho o dobro da idade que tu tinhas quando eu tinha o que tu tens.Quando tiveres a idade que eu tenho, a soma de nossas idades será de 45 anos.Quantos anos eu tenho?
no passado: minha idade =y, tua idade = z
atual: minha idade = x = 2z , tua idade = y
no futuro: minha idade = w, tua idade = x
Do enunciado:
w + x = 45
w = 45 - x (I)
x = 2z
z = x/2 (II)
Como todos envelhecemos juntos, as diferenças entre nossas idades atuais e do passado são as mesmas:
2z - y = y - z
3z = 2y
z = 2y/3 (III)
Pelo mesmo raciocínio, as diferenças entre nossas idades do futuro e atuais são as mesmas:
w - x = x - y
45-x -x = x - y
y = 3x - 45 (IV)
De (II) e (III):
x/2 = 2y/3
Usando (IV):
x/2 = 2(3x - 45)/3
x = 4(x - 15)
x = 4x - 60
-3x = -60
x = 20
Como y = 3x - 45, temos y = 3.20 - 45 = 15
Resposta: Tenho 20 anos e tu tens 15 anos.
Assinar:
Comentários (Atom)












